마지막 포스팅(엑셀로 만들어 보는 채권의 현금흐름표 4)에 엑셀 시트 첨부했습니다. 바쁘신분들은 아래 링크로 들어가시면 됩니다.
3. 채권의 듀레이션 및 만기수익률 등 수식 넣기
저번 포스팅에 이어 이번 포스팅은 만기수익률(YTM)과 듀레이션이 뭘 의미하는지 살펴보도록 하겠습니다.
만기수익률(YTM)은 만기까지 채권을 보유할 때, 미래의 들어오는 이자를 현재가치로 할인하여 채권 가격과 일치시킬 때의 이자율입니다. 또는 내부수익률(IRR)이라고 하기도 합니다. 만기수익률의 공식을 먼저 보고 천천히 살펴보겠습니다.
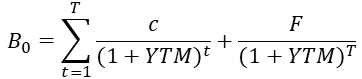
이 만기수익률은 매매 함에 있어 매우 중요합니다. 기호는 t = 기간, T = 만기, c = 이자금액, F = 원금, B0 = 채권가격입니다. 우리가 매입하려는 신세계건설 14의 채권 1개는 다음과 같습니다.
B0 = 10,250₩ (매입한 채권 가격)
c = 710₩ (표면이자율)
F = 10,250₩ (매입 원금)
t = 1 (연 단위 첫 1년 차)
T = 2 (연 단위 2년 만기 채권)
사실 T는 2가 아닙니다. 왜냐하면 우리가 매입하려는 채권은 1년에 이자 지급을 4번 하기 때문에 나누어야 하는 복잡함이 있어서 단순화 시켰습니다. 위 공식의 YTM은 손으로 구하기 매우 어렵기 때문에 엑셀의 함수를 사용해 보겠습니다.


위 사진은 우리가 매입한 금액 9,993,750₩은 실제 들어간 매입한 비용입니다. 그리고 초록색 부분이 IRR함수를 사용하여 만기수익률을 구하고 있습니다, 여기서 *4의 이유는 1년에 이자를 4번 지급받기 때문에 4를 곱해 주었습니다.
또한 만기까지 이자를 7회 받을 수 있고, 7회(만기) 때는 원금 즉, 채권 1개 당 10,000₩씩 해서 돌려받습니다. 채권 1개 당 10,250₩에 샀는데 만기에 10,000₩을 돌려받는다고 생각하니까 조금 손해 본 느낌입니다.
만기까지 우리는 4.644% 이자율로 기업에 돈을 빌려준 것이라고 생각하시면 그나마 마음이 편해집니다. 그리고 만기수익률을 사용할 때 3가지 특징이 있습니다.
1. 채권을 만기까지 보유해야 한다.
2. 이자수취액을 만기수익률로 재투자한다.
3. 채무불이행이 발생하지 않는다.
즉, 만기까지 보유하고 중간에 지급받은 이자를 4.644%의 만기수익률로 재투자해야 하며, 회사의 채무가 발생하지 않을 때, 만기수익률(YTM)은 의미가 있습니다. 보통 일상의 채권 수익률은 요구수익률(만기수익률)입니다.
채권 정보에는 액면이자율이 7.1% 였는데, 실제 우리가 만기까지 받을 이자율은 4.644%라고 하니까 별로 메리트가 없어 보이지만, 우리가 채권 가격을 10,250₩이 아닌 9,700₩에 샀다고 가정했을 경우, 만기수익률을 구해보면 조금 더 높게 나올 겁니다. 그리고 세금을 공제한 금액을 만기수익률의 현금흐름으로 사용했기 때문이기도 합니다.
다음은 듀레이션이 무엇인지 또 어떻게 구하는지 살펴보겠습니다.
듀레이션의 공식은 쓰지 않겠습니다, 매우 복잡하기도 하고 계산 방법과 개념만 알고 있으면 문제없습니다. 듀레이션은 쉽게 말해 원금 회수기간입니다. 간단한 예제를 살펴보겠습니다.
액면가 : 10,000,000₩
액면이자율 : 10%
만기 : 3년
만기수익률 : 9%
여기서 액면이자율 보다 만기수익률이 적은걸 보니 아마 액면가 보다 조금 비싸게 채권을 샀나 봅니다. 듀레이션의 계산 방법은 다음과 같습니다.
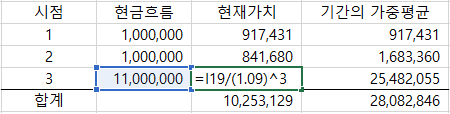
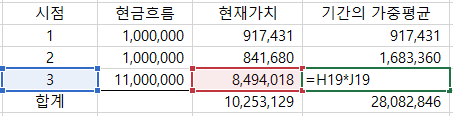
현재가치는 미래에 들어올 돈을 오늘의 이자율로 할인한 것 입니다. 1년 뒤 100만 원과 3년 뒤 100만원 중 선택하라고 하면 당연히 1년 뒤 100만 원을 선택할 겁니다. 이 처럼 액수가 같다면 빨리 수중에 돈이 들어오길 원하는 시간 선호현상이 일어납니다. 3년 뒤 300만 원으로 바뀐다면 달라질 것입니다. 그럼 위 표를 가지고 듀레이션을 구하는 방법은 다음과 같습니다.
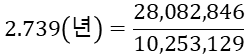
기간의 가중평균한 값의 합계와 현재가치의 합계를 나누기만 하면, 우리가 원금을 회수하는 기간인 듀레이션을 구할 수 있습니다. 저는 처음에 많이 어려웠지만 이해하고 나니 쉬운 개념이었습니다. 수고하셨고 읽어주셔서 감사합니다
'월 스트리트 > 채권' 카테고리의 다른 글
| 제이알글로벌리츠 채권 은행 이자보다 높은 이자를 매월 받는 제이알글로벌위탁관리부동산투자회사2 (0) | 2023.09.29 |
|---|---|
| 채권 투자 방법과 채권의 특징 (0) | 2023.09.26 |
| 엑셀로 만들어 보는 채권의 현금흐름표 4 (0) | 2023.09.20 |
| 엑셀로 만들어 보는 채권의 현금흐름표 2 (0) | 2023.09.19 |
| 엑셀로 만들어 보는 채권의 현금흐름표 1 (0) | 2023.09.18 |



